[ML] GBM (Gradient Boosting machine)

최근에 ML기반의 모델에서 좋은 성능을 보이는 LGBM에 대해서 뜯어보자.

그 전에, Boosting의 기본적인 특성을 알아하는데, https://life-of-h2i.tistory.com/37 여기에서!

 

간단하게만 정리하면,

부스팅은 weak한 모델을 여러개 이용하여 좋은 결과를 얻는 방식이다.

(단, 여기서 이용되는 모델들은 Seqeuntial하게 전자의 모델이 못 맞춘 부분을 맞추는 방식으로 생성된다.)

---

GBM (Gradient Boosting Machine)

GBM은 제목에서 알수있듯이 'Gradient Descent' + 'Boosting'이 합쳐진 것이다.

Boosting은 알고 있으니, Gradient Descent를 간단히 살펴보자.

 

1. Gradient Descent

https://life-of-h2i.tistory.com/48 미분의 이용

한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야 함수값이 증가하는지/감소하는지 알 수 있다.

미분값을 빼면 경사하강법(gradient descent)이라 하며 함수 값이 감소한다. -->  함수의 극소값의 위치를 구할 때 사용한다.

 

2. Gradient Boosting

부스팅 기법은 전자의 모델이 못맞춘 부분을 포커스해서 맞춘다고 설명했다.

GBM모델은 전자의 모델이 맞추지못한 부분, 즉 실제값 - 예측값 (Loss) 를 다음의 모델이 맞춘다.

다음 그림에서,

원래 Original Dataset에 대해 f1(x) 가 어떤 값을 예측했다.

그러면 f2(x)는 f1(x)가 예측하고 남은 부분을 예측한다.

이것을 계속 반복한다.

 

그럼, 여기서 질문! Gradient descent는 어디에 쓰이는 건가.

 

맞다. 사실은 저 빼기에 이미 gradient descent 가 사용되었다.

우리가 직관적으로 y-f(x)를 사용하는것은 사실 Squared error loss 의 미분값이다.

 

Squared error 란, 단순하다.

다음과 같이 빨강, 파랑 점이 진짜 값이고, 검은색 선이 예측값이라고 생각해보자.

실제값과 예측값의 차이는 어느정도일까? 라는 질문에

" (실제값 - 예측값) ^ 2 " 라고 하는게 MSE loss 이다. 이걸 식으로 적으면 다음과 같을것이다.

(참고로 1/2가 곱해진건, 미분할때 쉽게 하기위한 트릭이다.)

MSE loss

 

그럼 Gradient descent를 구하기 위해 이 MSE loss를 미분해보자. 

L 이 MSE loss식이다. 그럴때 다음과 같이 미분될 것이고, 이는 f(x)-y 이다.

여기에 - 방향으로 빼줘야하므로 -(f(x)-y) = y-f(x) 가 된다.

 

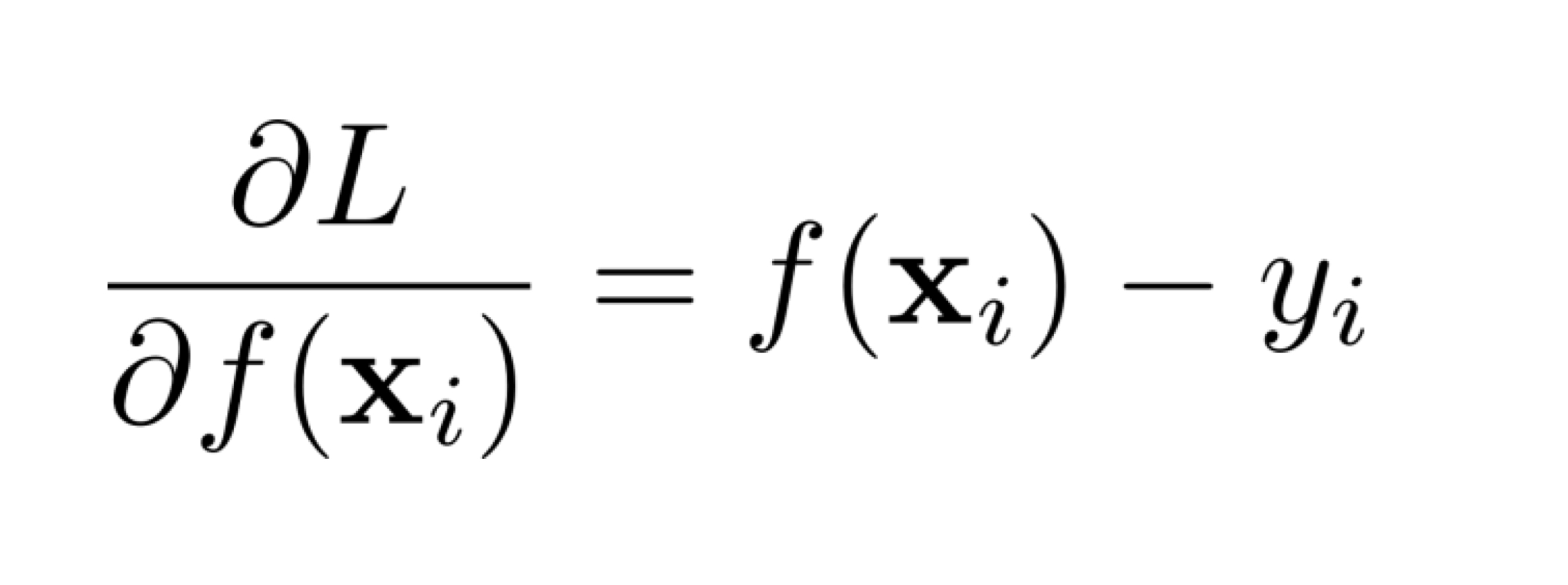
뭐언가 연결이 될듯말듯, 알듯말듯하다.

 

이럴때, pseudo code를 보자.