[부캠] 베이즈 통계학 맛보기

• 조건부 확률
• 베이즈 정리
• Confusion Matrix
• Naiive Bayse

 

---

조건부 확률

조건부확률

조건부확률 P(A|B)는 사건 B가 일어난 상황에서 사건 A가 일어날 확률을 의미한다.

 

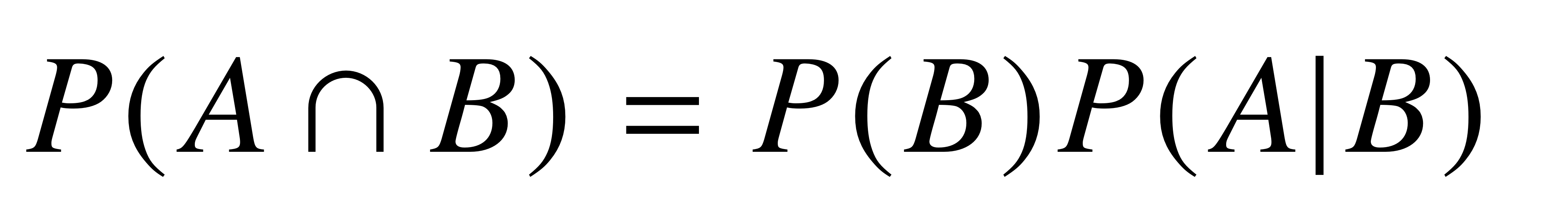
조건부확률과 인과관계

많은 사람들이 조건부확률을 인과관계로 해석한다.

예를들어 P(A|B) 가 0.9로 높은 확률이라하자.

그렇다면 A와 B는 강한 인과관계를 가지고 있다고 할수 있을까?

 

아니다.

 

조건부 확률은 유용한 통계적 해석을 제공하지만, 인과관계를 추론할때 함부로 사용해서는 안된다.

왜냐하면 '중첩요인'에 의해 '가짜 연관성'이 생길수 있다.

 

예를들어,

치료법 a,b의 완치율에 대한 인과관계를 파악하고자 한다고 하자. (R : 완치(1), A : 치료법 a, B : 치료법 b)

보다싶이 신장 결석 크기에 상관없이 전체로 조건부 확률을 구하면,  P(R=1|A) < P(R=1|B) 이다.

하지만, 신장 결석 크기로 나누어 확인했을 때, 크기에 상관없이 A가 더 높은 완치율을 보였다.

이렇게 '신장 결석크기'는 치료법과 완치여부에 둘다 영향을 주는 중첩요인이다.

이 중첩요인때문에 가짜연관성이 생겨 왜곡된 결과를 보여주게 된다.

 

가짜연관성 해결법 (조정효과)

그래서, 조건부 확률로 인과관계를 따질때는 매우 조심해야한다.

그 중, 조정효과를 통해서 중첩요인의 개입을 제거하는 방법을 소개한다.

신장 크기 예시에서

다음과 같이 계산해 Z의 개입을 제거한다.

---

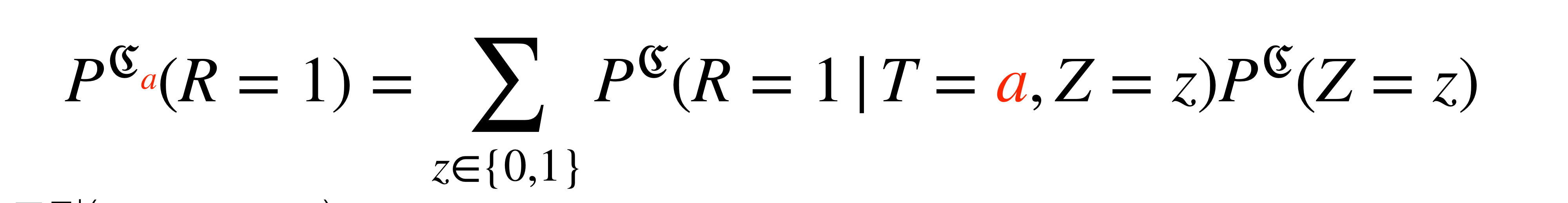
베이즈 정리

베이즈 정리는 조건부확률을 이용하여 정보를 갱신하는 방법을 알려준다.

P(B|A)를 P(A|B)를 통하여 나타내보자.

기존의 B라는 현상이 있을때, A라는 새로운 정보가 주어졌다고 하자.

이때, P(B)를 통해 P(B|A)를 계산할 수 있다.

 

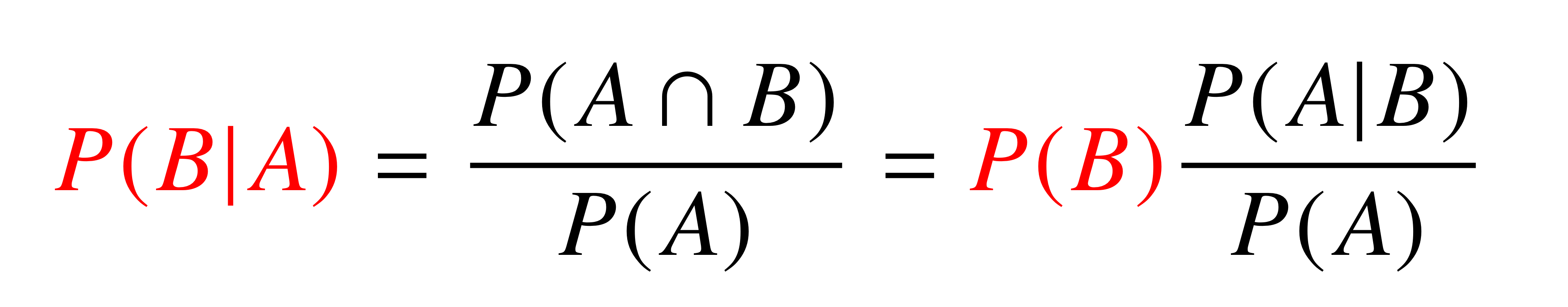
이것을 우리의 확률분포에 적용해보자.

데이터셋 D에 대해서 θ 가 성립할 확률을 구하고 싶다고 한다면,

이는 θ에 대한 사전확률, likelihood, Evidence로 구할 수 있다.

라고 말하면 너무 어렵다. 예시를 보자

 

Q. Covid 발병률이 10%로 알려져있다. Covid 에 실제로 걸렸을 때 검진될 확률은 99%, 실제로 걸리지 않았을 때 오검진될 확률이 1%라고 할 때, 어떤 사람이 질병에 걸렸다고 검진결과과 나왔을 때 정말로 Covid 에 감염되었을 확률은?

 

 

A.

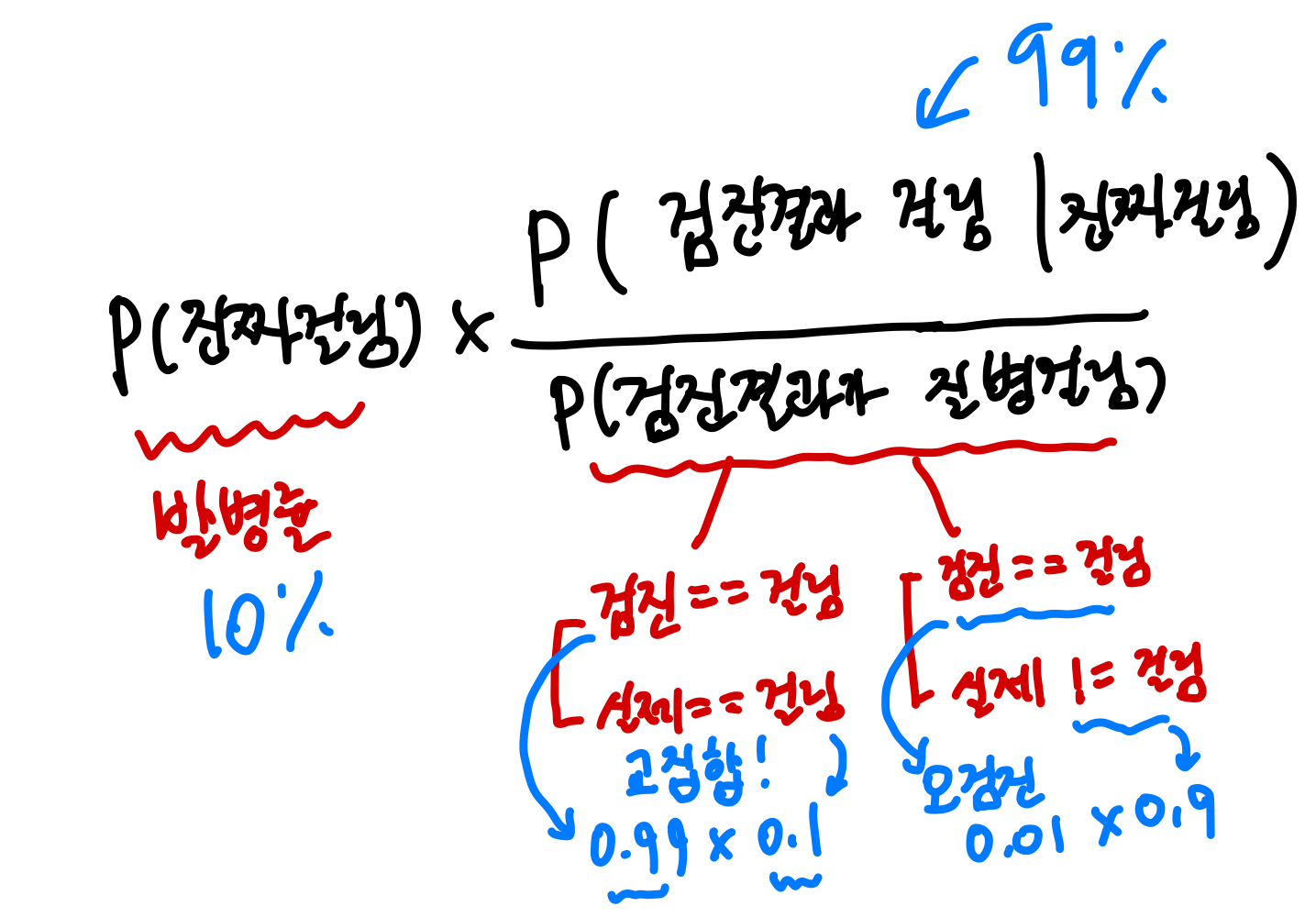
구하고자 하는 것 P ( 진짜 걸림 | 검진결과==질병걸림)

여기서, 베이즈 정리에 의해 다음과 같이 유도가 된다.

 

이렇게 새로운 데이터가 추가 되었을 때, 해당 데이터에 대한 θ가 성립될 확률을 알고싶다면

과거의 확률분포 정보를 활용해서 구할 수 있다.

 

베이즈 정리를 통한 정보의 갱신

베이즈 정리를 이해하고 나서, 든 의문.

'아니 그러면 초반에 θ를 잘~~ 아주 잘~~ 구해야 의미가 있는거 아닌가? θ가 엉망진창이면, 당연히 정확도가 낮은거 아닌가?'

 

베이즈 정리는 계속해서 새로운 데이터가 들어왔을 때 과거의 사후확률 (posterior)를 사전확률(priori)로 사용해 갱신된 사후 확률을 계산할 수 있다.

즉, θ 에 대한 확률분포를 지속적으로 업데이트 할 수 있다.

이렇게 갱신을 하면서 점점더 좋은 θ를 갖을 수 있다.

---

Confusion Matrix

요건 면접에 자주나와서 따로 뺏다. ㅎㅎ

안잊어버리기 위해, 직접 써본당..

Binary classification에서 자주 쓰는 metric이다.

베이즈 정리와도 연관이 꽤 있다. Evidence를 구할때 우리는 TP 와 FP 를 더해준다. 

따라서 precision(정밀도)을 구하면 사후확률이 어느정도일지도 예측이 되는것이다.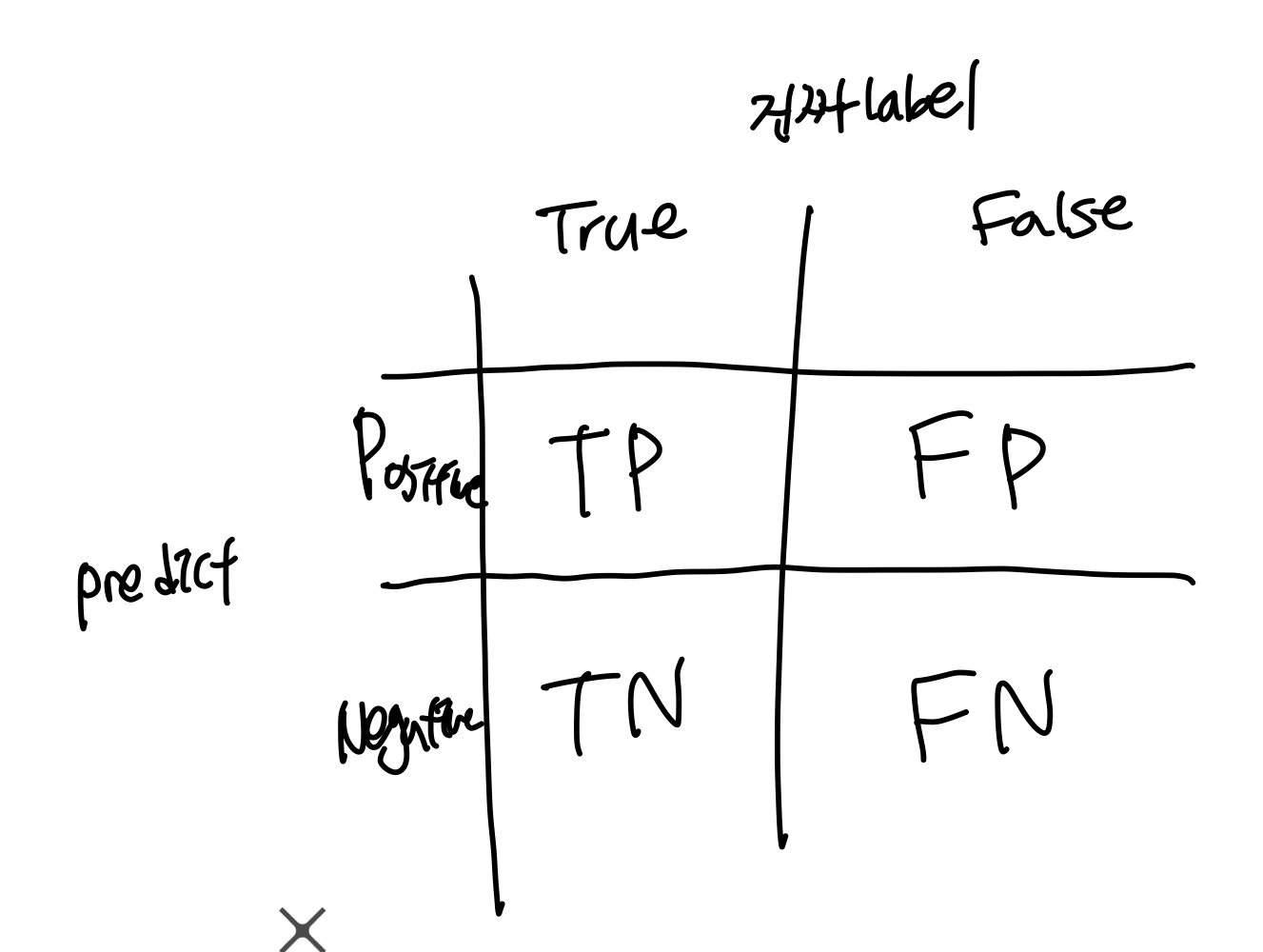

---

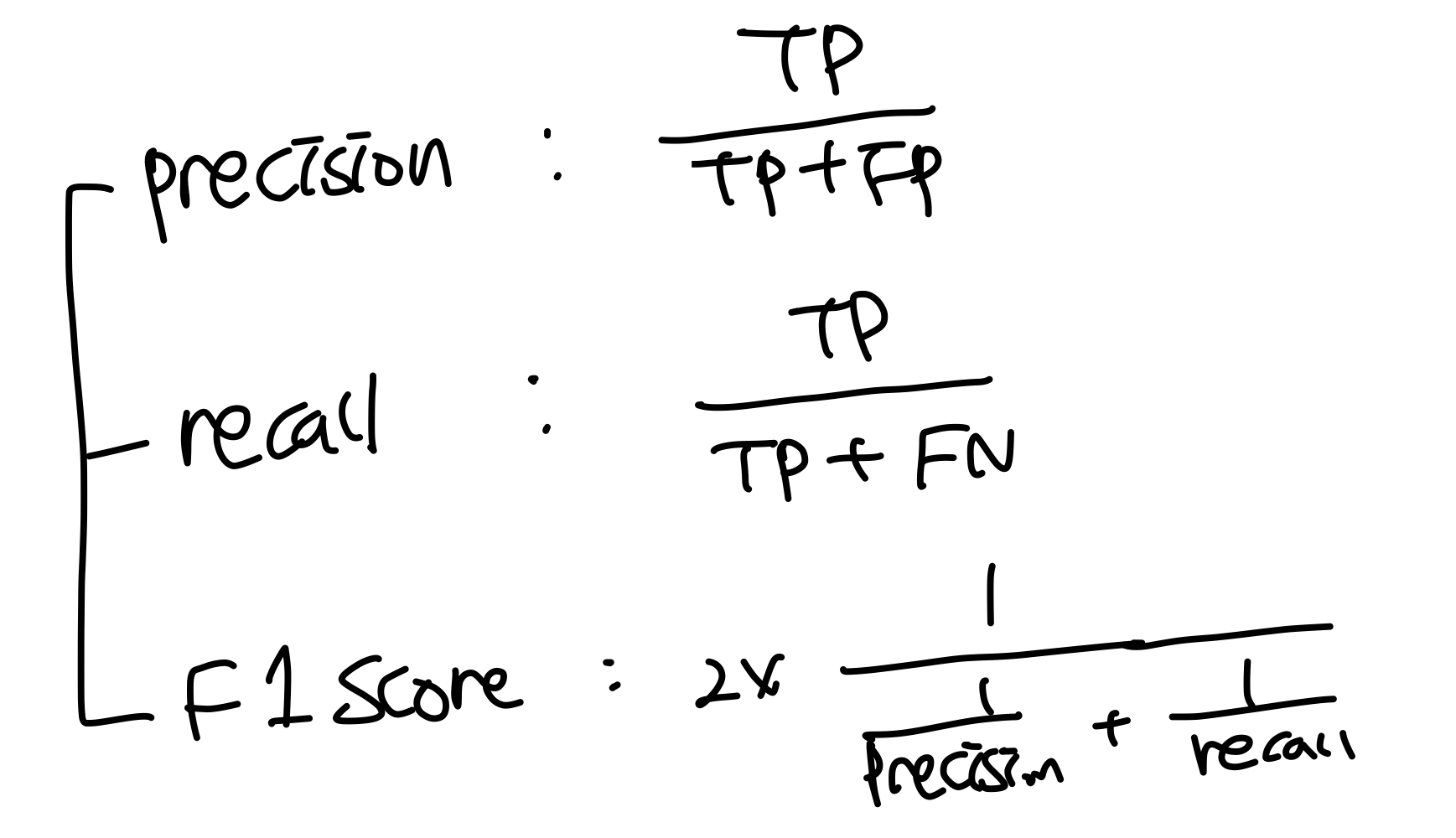
Naiive Bayse classifier

빠르게 브리핑.

지금까지 예시를 보면 베이즈 정리는 D가 1차원에만 맞춰져있는 것을 알 수 있다.

하지만, 베이즈 정리는 다차원 데이터 D에도 당연히 적용이 가능하다.

 

Likelihood를 구하는 과정 (P(D|θ)=P(d1,d2,d3,,,|θ)만 잘 구한다면..!

Naiive bayse는 데이터의 피쳐들이 모두 독립적이라고 가정한다.

따라서, 

A,B  가 독립적일때 P(A|B)=P(A) , P(B|A)=P(B)라는 특성과 chain rule을 통해

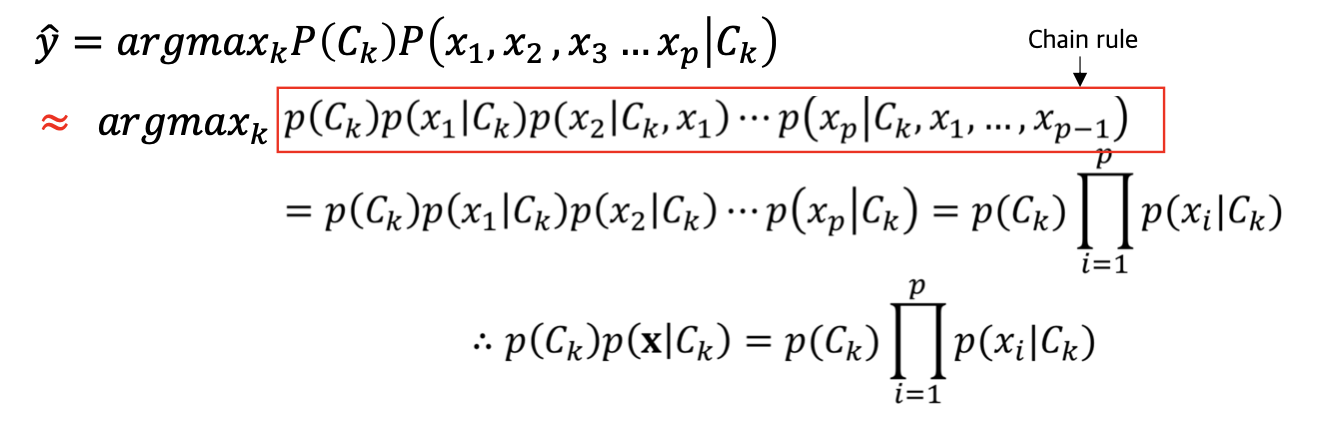
likelihood가 θ에대한 각각의 피쳐가 일어날 조건부 확률의 곱으로 바꿀 수 있다.

 

🍜