[부캠] Numpy의 기본 이용 & 백터와 행렬
- Numpy
- 벡터
- 행렬
노랑색 : 내용 추가 (개인적으로 더 알아볼것)
분홍색 : 질문 (이해가 안되는 부분)
1. Numpy
1-1. ndarray
numpy 는 np.array를 활용하여 배열을 생성한다.
파이썬은 기본적으로 리스트를 제공한다.
배열과 리스트의 차이점은 저번에도 말했지만 다음과 같다.
배열은 메모리 자료구조 안에 값이 바로 들어있지만, 리스트는 해당 값이 있는 주솟값이 들어있다.

배열의 shape & shape 변경(reshape / flatten)

import numpy as np
a = np.array([1, 2, 3, 4, 5])
#array([1, 2, 3, 4, 5])
a.shape
# (5,)
a.dim
# 1
a = np.array([1, 2, 3, 4, 5,6])
#array([1, 2, 3, 4, 5, 6])
np.array(a).reshape(2,3)
#array([[1, 2, 3],
[4, 5, 6]])
# -1은 나머지 argument에 맞춰 숫자를 알아서 조정해줌.
np.array(a).reshape(-1,3)
#array([[1, 2, 3],
[4, 5, 6]])
np.array(a).reshape(-1,3).flatten()
#array([1, 2, 3, 4, 5, 6])
배열의 인덱싱, 슬라이싱
배열은 2가지 방법으로 indexing을 표기한다.
array[row][col]
또는
array[row,col]
test_exmaple = np.array([[1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8]], int)
test_example[0][0]
#1
test_example[0,0]
#1배열은 행과 열을 나누어서 slicing을 한다.
test_exmaple = np.array([[1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8]], int)
test_exmaple[:,2:] #행전체 2열이후
#array([[5, 8],
[5, 8],
[5, 8],
[5, 8]])
test_exmaple[:,::2] # ::2 --> :(start):(end)2(hop) 행전체 열 처음부터 끝까지 2칸 띄면서
array([[1, 5],
[1, 5],
[1, 5],
[1, 5]])배열의 연산
numpy는 배열간의 다양한 연산을 제공한다.
test_a = np.array([[1, 2, 3], [4, 5, 6]], float)
test_a + test_a
#array([[ 2., 4., 6.],
[ 8., 10., 12.]])
test_a - test_a
#array([[0., 0., 0.],
[0., 0., 0.]])
test_a * test_a
#array([[ 1., 4., 9.],
[16., 25., 36.]])
그중에서 짚고 넘어가야할 2개가 있다.
elementwise product 와 dot-product
elementwise product는 배열들의 같은 위치에 있는 원소들끼리 곱하는 것을 의미한다.
dot-product는 우리가 일반적으로 알고 있는 내적계산을 의미한다. numpy에서는 dot 또는 @ 로 계산을 한다.
test_a = np.array([[1, 2, 3], [4, 5, 6]], float)
test_b = test_a.reshape(3,2)
test_a
#array([[1., 2., 3.],
[4., 5., 6.]])
test_b
#array([[1., 2.],
[3., 4.],
[5., 6.]])
#element wise product
test_a * test_a
#array([[ 1., 4., 9.],
[16., 25., 36.]])
#dot product
np.dot(test_a,test_b)
#array([[22., 28.],
[49., 64.]])
test_a @ test_b
#array([[22., 28.],
[49., 64.]])
2. 벡터
벡터의 의미
벡터는 숫자를 원소로 가지는 리스트 또는 배열이다.
vector = [1,2,3,4,5]벡터는 공간(n차원)에서의 점을 의미한다.
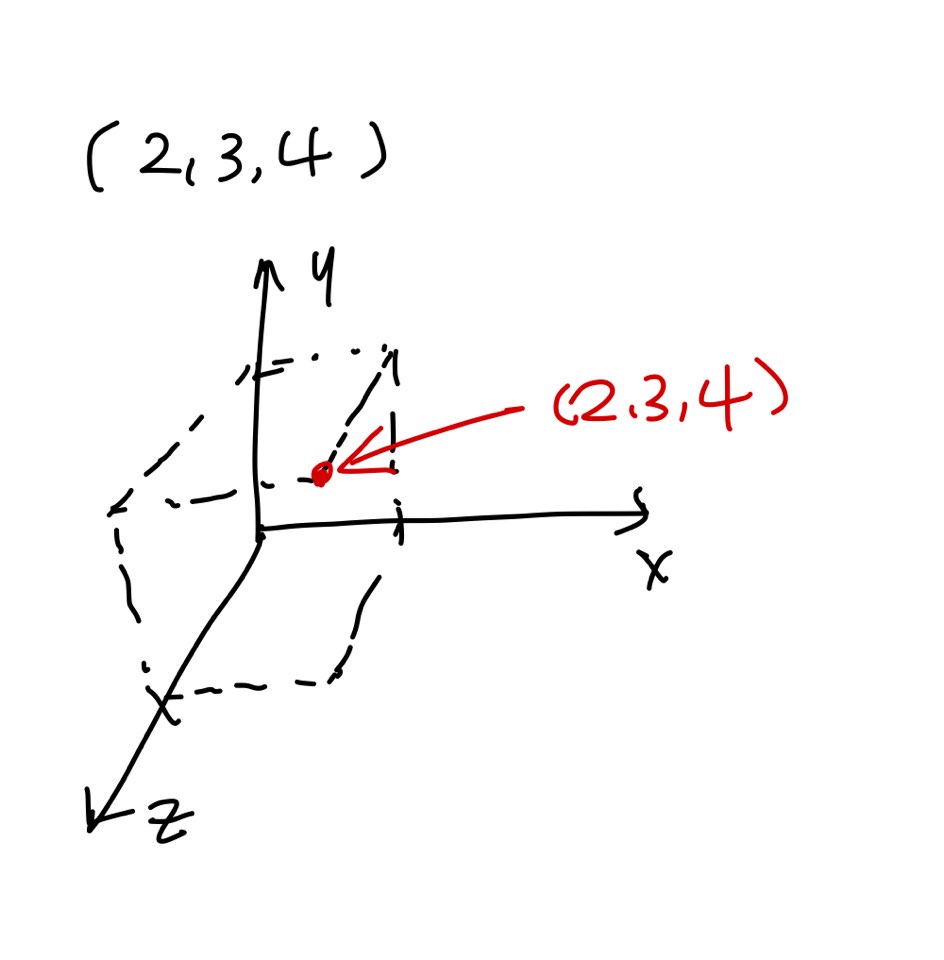
벡터의 거리
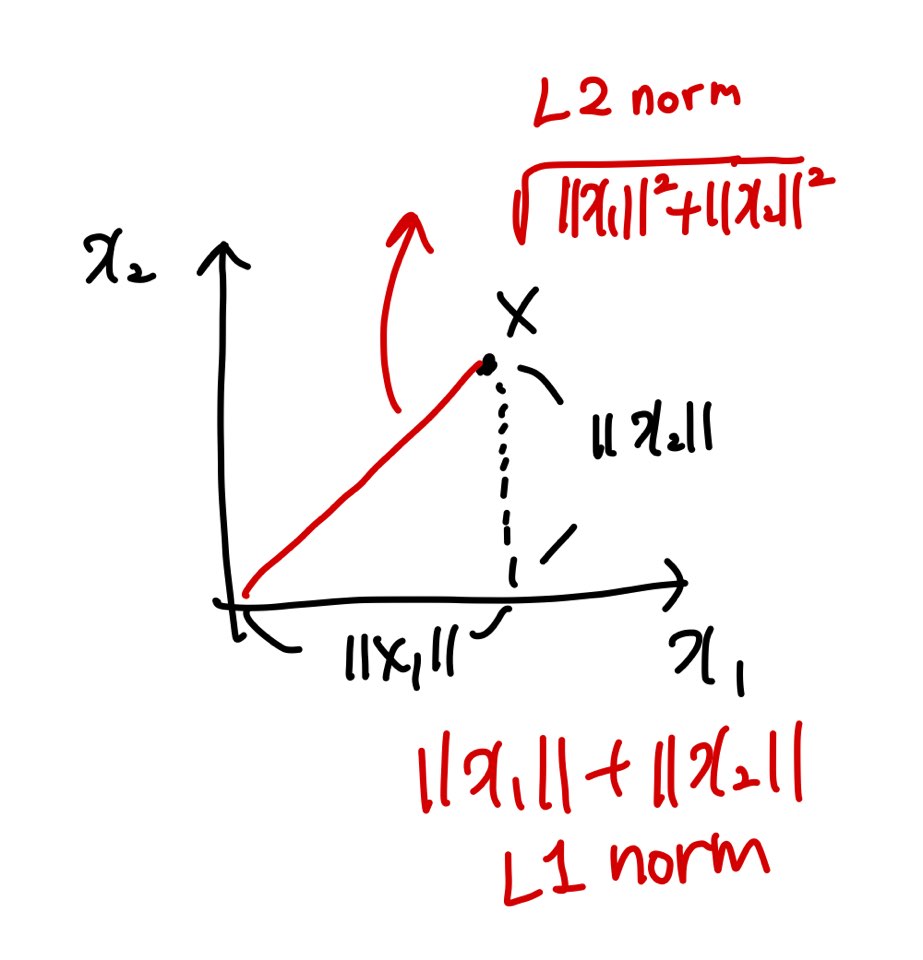
벡터의 거리를 구하는 방법은 2가지가 있다.
- L1 norm : 원점으로부터 벡터의 성분의 절댓값의 합
- L2 norm : 유클리드 거리
L1 norm 과 L2 norm은 서로 다른 기하학적 의미를 가지고 있으며,
이 의미는 각종 regression에 사용된다.
ex) L1 norm : Lasso 회귀
L2 norm : Laplace 근사, Ridge 회귀
두 벡터의 각도
코사인 제 2법칙을 활용하여 두 벡터의 각도를 구할 수 있다.

3. 행렬
행렬은 여러 벡터로 이루어진 2차원 배열이다.
행렬의 의미
행렬은 여러 벡터로 이루어져 있으므로, 여러 점들을 의미한다.
또한 행렬은 벡터 공간에서의 연산자로 활용된다. 행렬곱을 통해 벡터를 다른 차원의 공간으로 이동시킬 수 있다.

역행렬
어떤 행렬 A의 연산을 거꾸로 되돌리는 행렬을 역행렬이라한다.
-역행렬은 행과 열 숫자가 같아야하고, 0이 아닌 행렬이어야한다.
-역행렬은 곱하는 순서에 상관없이 항상 성립한다.
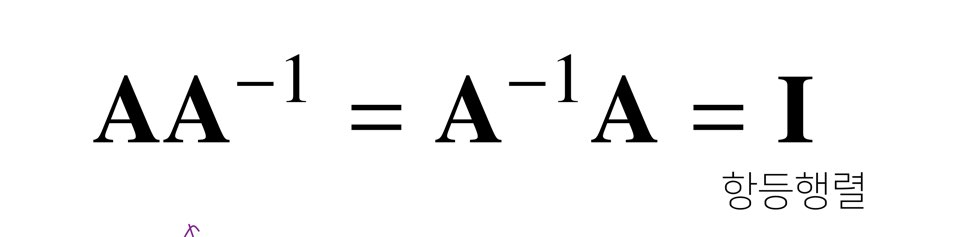
test_matrix = [[1, -2, 3], [7, 5, 0],[-2, -1, 2]]
test_matrix = np.array(test_matrix)
np.linalg.inv(test_matrix)
#array([[ 0.21276596, 0.0212766 , -0.31914894],
[-0.29787234, 0.17021277, 0.44680851],
[ 0.06382979, 0.10638298, 0.40425532]])
test_matrix @ np.linalg.inv(test_matrix)
#array([[ 1.00000000e+00, -1.38777878e-17, 0.00000000e+00],
[ 0.00000000e+00, 1.00000000e+00, -5.55111512e-17],
[-2.77555756e-17, 0.00000000e+00, 1.00000000e+00]])유사 역행렬
그렇다면, 행과 열 숫자가 같지 않은경우에는 어떻게 역행렬을 구해야할까?
이때는 유사 역행렬(무어 펜로즈 역행렬)을 이용한다.
단, 행과 열의 크기에 따라 연산의 순서가 다르다.

test_matrix = [[1, -2, 3], [7, 5, 0]]
test_matrix = np.array(test_matrix)
np.linalg.pinv(test_matrix)
#array([[ 0.09250243, 0.09834469],
[-0.12950341, 0.06231743],
[ 0.21616358, 0.00876339]])
test_matrix @ np.linalg.pinv(test_matrix)
#array([[ 1.00000000e+00, 1.12757026e-16],
[-2.77555756e-17, 1.00000000e+00]])